投资回报率怎么算,

导读： 相信大多数人在日常理财中都会遇到这样一个问题，就是复利的计算很麻烦。 的确，如果年化收益是X%，n年后的收益就是(1+x%) n。 就这样，没有计算器，恐怕一时半会儿很难算出来。 金融学上有所谓的72法则、71法则、70法则、69.3法则，用来估计投资的翻倍或减少。

投资回报率怎么算,

相信大多数人在日常理财时，都会遇到这样的问题，就是"复利的计算很麻烦"。

的确事实也是这样，如果年化收益是

X%

，那N年以后的收益是

(1+X%)^N

。这样，没有计算器，恐怕一时半会儿很难算出来。

金融学上有所谓

72法则、71法则、70法则和69.3法则

，用作估计将投资倍增或减半所需的时间，反映出的是复利的结果。

今天我们先来聊一聊

72法则

。

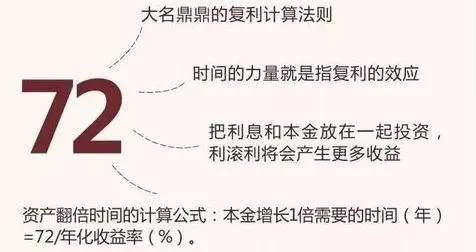
其实72法则就是以1%的复利来计息，经过72年之后（72是约数，准确值是ln2/ln1.01），本金会变为原来的一倍，这个公式的好处在于能够以一推十。

这个公式可以快速

用来计算在给定的年收益的情况下，大约需要多少年，我们的投资才会翻倍。

具体计算过程如下：

（1）决定你的投资回报的年利率；

（2）用72除以年利率（%）；

（3）结果就是你的投资倍增所需的年数。

例如：

一个人在股市中投资10万美元，投资回报的

年利率为10%。

72法则的计算过程如下：

第一步：

10万美元原始投资的年利率为10%；

第二步

：

用72除以10;

第三步：

得到7.2

结果：

7.2年后10万美元变成20万美元。

如果这个人不动用利润和本金，10万美元的原始投资在7.2年后将倍增为20万美元，14.4年后将成为 40万美元，21.6年后将成为80万美元，28.8年后将成为160万美元，依此类推。

之所以选用72，是因为它有较多因数，容易被整除，更方便计算。它的因数有

1、2、3、4、6、8、9、12

和它本身。

一般息率或年期的复利

使用72作为分子足够计算一般息率（由6至10%），但对于较高的息率，准确度会降低。

关于72法则的计算，文章末尾有放置了72法则的推导过程，对数字和计算过程比较感兴趣的读者可以阅读思考。

这时候就会有朋友问，既然用起来这么方便，那72法则计算真的准确吗？

了解他们之间的误差，以及使用范围，我们才能在实际运用中心中有数，运用起来才有底气。我这里使用EXCEL计算出了二张表格，可以对比一下72法则与精确计算之间的误差。

下表是在规定年限内企业的总收益翻了一倍，来计算企业的平均年收益率。

当企业1年收益翻1倍时，72法则的年收益率为

72%

，而精确计算为

100%

，误差最大，为

28%

。其实在1年内企业收益翻1倍根本没有必要计算了，年收益率当然是

100%

了。

当企业在2年内收益翻了1倍时，72法则计算得出平均年收益率为

36%

，而精确计算为

41.42%

，误差为

5.42%

。

当企业在3年内收益翻了1倍时，72法则计算得出平均年收益率为

24%

，而精确计算为

25.99%

，误差为

1.99%

。

可以看出前面三项误差最大，只要把前面三项的误差记住了，而后面的计算误差不会超过1%，已经很小了，可以忽略不计。所以使用72法则来估算是符合实际的。

上表计算了在规定年限内收益翻一番时的平均年收益率。

下表是以平均年收益率来计算多少年才能让总收益翻一番？

从以上两表可以看出，使用收益率来计算总收益翻一倍的年数差误是比较小的，可以直接使用72法则。

使用在规定年内总收益翻一倍的平均年收益率时，

只要年数大于3年，72法则计算出来的精确度是比较高的。在实际运用中只需要记住前面三项误差，然后进行适当的校正，就能直接使用72法则了。

使用72估算法则，可以让我们在价值投资中迅速估算企业的年收益率或者年收益增长率。

大价值投资中经常要计算的年收益率或者年增长率这些指标，72法则为我们提供了一很好的估算方法。

感兴趣的读者可以看一下公式的具体推算过程：

定期复利的将来值（FV）为：

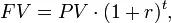
当中PV为现在值、t为期数、r为每一期的利率。

当该笔投资倍增，则FV = 2PV。代入上式后，可简化为：

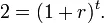
解方程式，t为：

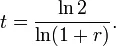
若r数值较小，则

ln(1+r)

约等于r（这是泰勒级数的第一项）；加上

ln(2) ≈ 0.693147

，于是：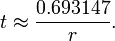

总结：以上内容就是对于投资回报率怎么算,的详细介绍，文章内容部分转载自互联网，希望对您了解投资回报率怎么算有帮助和参考的价值。